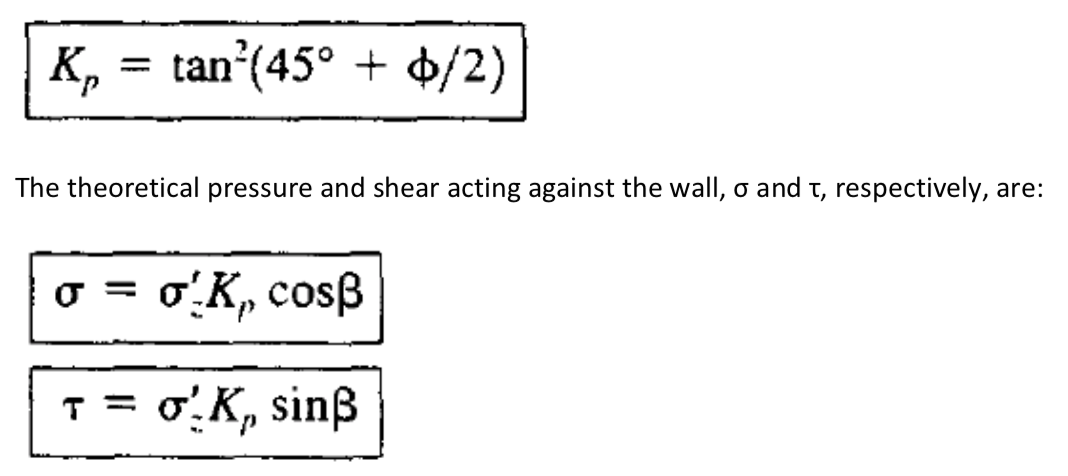Rankine为主动/被动压力的地球压力理论的假设
兰诗的地球压力理论
如最初提出的,兰诗的理论仅适用于均匀的内聚力土壤。后来,它延伸到1915年贝尔的粘性土壤。
兰宁理论的假设:
Rankine通过以下假设接近横向的地球压力问题:
- The soil is homogeneous and isotropic, which means c, φ and γ have the same values everywhere, and they have the same values in all directions at every point (i.e., the strength on a vertical plane is the same as that on a horizontal plane). This discussion will be expanded later to consider layered soils, where each layer has different values of c, φ and γ∙
- 最关键的剪切表面是平面。实际上,它略微凹陷,但这是一个合理的假设(特别是对于有源案例),它简化了分析。
- 地面是平面(尽管它不一定需要等级)。
- 墙无限长,因此可以仅在两个维度下分析问题。岩土科工程师将此称为平面应变条件。
- 墙壁足够移动以发展主动或被动条件。
- 作用在壁背面的正常和剪切力的所得到的成果以平行于地面的角度倾斜(库仑理论提供了一种在墙壁上作用的更准确的剪切力模型)。
积极的条件
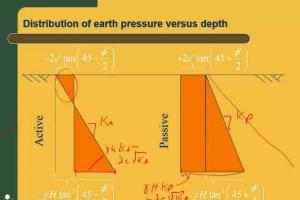
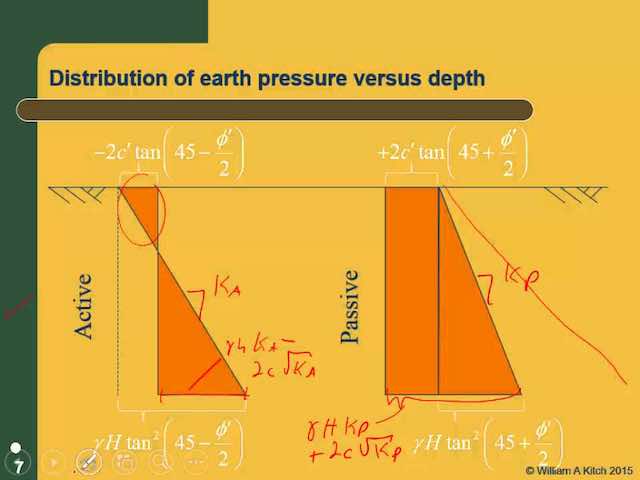
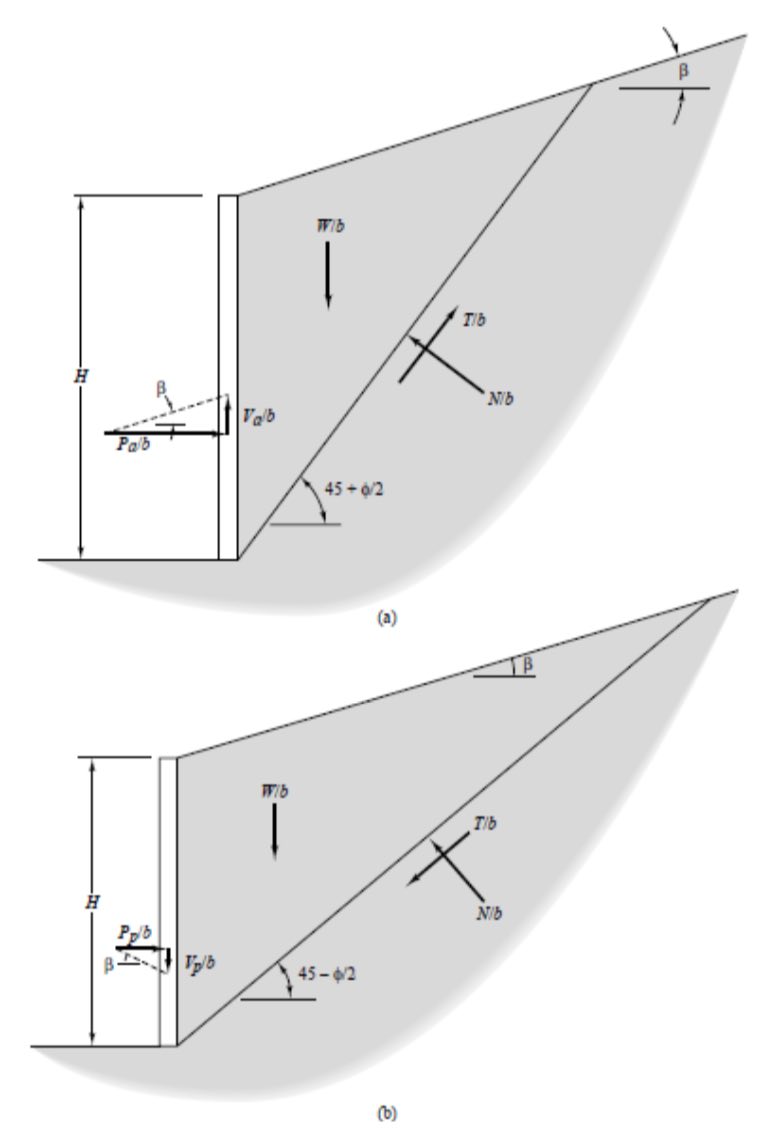
通过这些假设,我们可以将墙壁后面的土壤楔形作为自由体,并使用静态原理评估问题,如图1A所示。这类似于用于分析地球斜率稳定性的方法,并且被称为极限平衡分析,这意味着我们认为如果沿着故障楔的底部即将失效的土壤即将失效,则认为该条件将发生在剪切中。土壤中的弱接缝或其他非均匀性可以控制临界剪切表面的倾斜度。但是,如果土壤是均匀的,p一种当该表面与水平45 +φ/ 2度的角度倾斜时,/ b最大,如图所示Mohr的圈子。因此,这是最关键的角度。
解决PA / B和VA / B的免费体图给出:
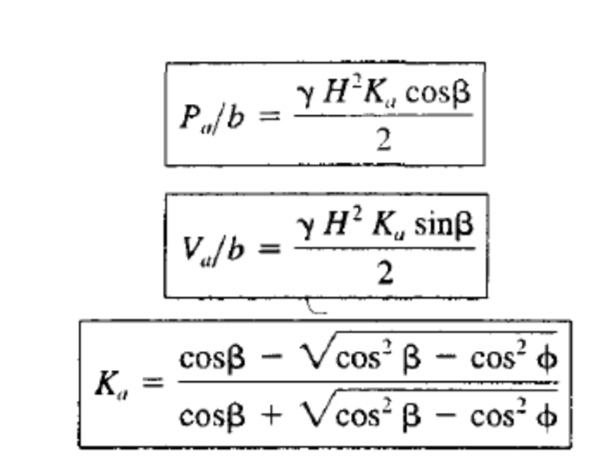
Ka的大小通常在0.2和0.9之间。仅当β≤φ时,等式仅有效。如果β= 0,则降低:
PA / B作为H的溶液将表明理论压力分布是三角形的。因此,分别作用靠壁,α和τ的理论压力和剪切应力是:
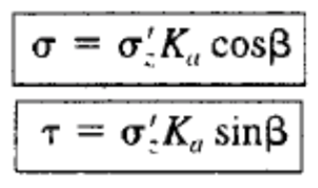
在哪里;
σ=从土壤挡土墙上施加的土壤压力
τ=剪切应力赋予挡土墙从土壤中的挡土墙
PA / B =每单位长度的土壤和墙壁之间的正常力
va / b =每单位长度的土壤和墙壁之间的剪切力
B =墙的单位长度(通常是1英尺或1米)
ka =横向地球压力σz的主动系数=垂直有效应力
β=墙壁上方地面的倾斜度
H =墙壁高度
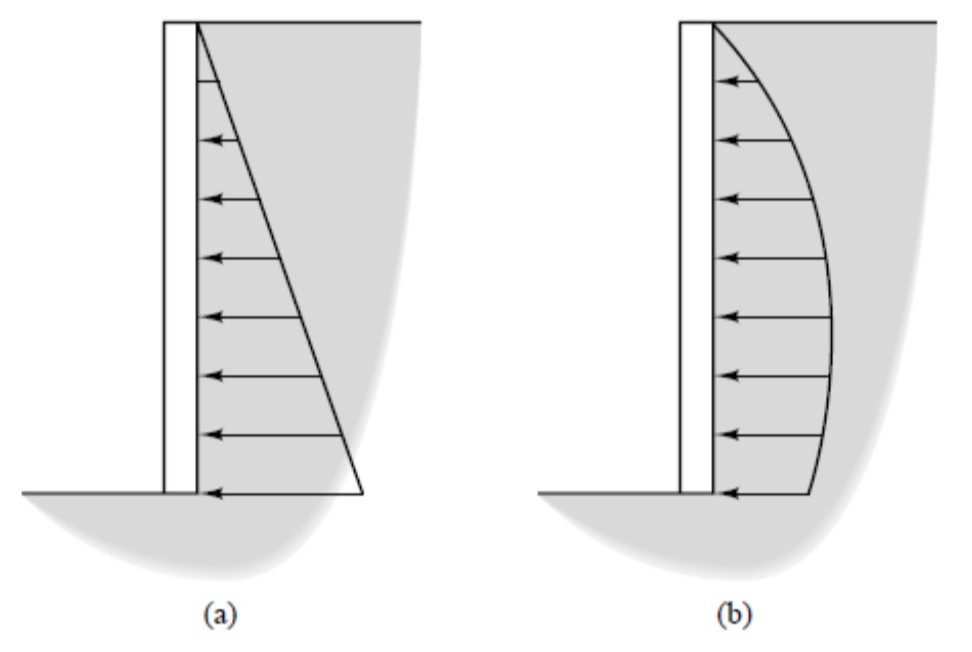
然而,来自真实保留结构的观察和测量结果表明真正的压力分布,如图2所示,不是三角形的。这种差异是因为墙壁偏转,拱形和其他因素。PA / B和VA / B的幅度大致正确,但是由理论预测的底部的约0.40h的所得作用(Duncan等,1990)。
被动条件
Rankine以类似于主动条件的方式分析了被动条件,除了沿着楔形底的剪切力沿相反方向作用(它总是反对楔形的运动),并且自由体图变得如图所示图1b。请注意,故障楔子比在活动案例中的变得大大变得大得多,并且临界角度现在是水平的45 - φ/ 2度。分别在无源壳体中作用在墙壁上的正常和剪切力,PP / B和VP / B是:
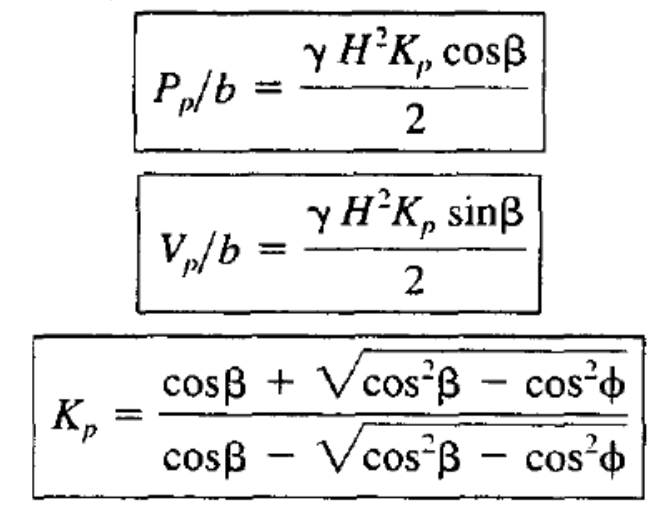
仅当β≤φ时,等式仅有效。如果β= 0,则降低: