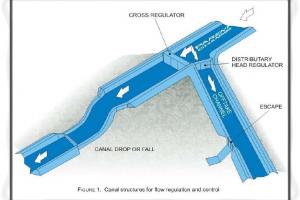
Khosla的液压结构理论

在研究基于的大量坝故障之后Bligh的理论，Khosla与他自己的调查结果出来了。以下是其中一些主要观点Khosla的理论

通过观察在Bligh理论上设计的虹吸管，通过实际测量压力，借助插入的管道在两个虹吸管的地板上没有显示出与Bligh的理论上计算的压力的任何关系。这导致以下临时结论：

• 端板桩的外面比内部纸张和地板的水平长度更有效。
• 除局部重新分布的压力外，较小长度的中间桩无效。
• 破坏地面从尾端开始。
• 在下游端具有相当深的垂直切断是绝对必要的，以防止破坏。
• Khosla及其同事考虑了液压结构不可渗透的底部的流动模式，以计算隆起压力和出口梯度。
• 从一个简单的水平流动的情况下，宽度较小的厚度。（数学分析各种病例。）
• 液压结构下方的渗水不遵循不受折射的不透水地板的底部轮廓，但每个粒子沿着一系列流线追踪其路径。

对于直线下的二维流量的情况：

因此，对于触摸地板轮廓的第一流线AB，可以通过在等式中放置不同的X值来获得压力。图4通过等式4以及Bligh的理论来表示压力分布直径。从图中可以得出以下结论：

压力图的斜率：在无限的A和B处，因此A的地板将是理论上的无限作用，在B时也将是无限的。这将导致沙子沸腾，因此应在下游端提供抑郁或切断地板。

综合简介：

在Khosla的理论中考虑了以下一般形式的具体原因

• 直线水平流动可忽略不计的厚度，在任何一端，上游或下游端都有绒头。
• 在一些中间点处具有桩的厚度可忽略不计的水平地板。
• 直线水平楼层，郁闷在床下，但没有切断。

独立变量的方法：

• 大多数设计不确认基本配置文件（具体情况）。在实际情况下，我们可以在上游水平，下游水平和中间点以及地板上具有一些厚度。
• Khosla通过称为独立变量方法的经验方法解决了实际问题。
• 该方法包括将复杂的简档分解为多个简单的简档，每个简单的轮廓是独立的和数学治疗的。然后施加校正由于地板坡度的厚度。
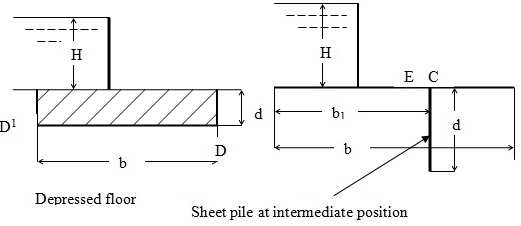
• 作为示例，图中所示的复杂轮廓被破坏到以下简单的简单轮廓和所获得的关键点处的压力。
• 在上游末端的厚度可忽略不计的底部。
• 直线厚度可忽略厚度，下游桩桩。
• 直线厚度可忽略的厚度，中间点桩。
• 通过考虑简单的轮廓，在关键点处获得压力。

对于低于液压结构的渗漏的测定开发了独立变量的方法。
在这种方法中，a的实际配置文件堰这是复杂的，分为一个数字简单的简档，每个轮廓都在数学上解决而不是很困难。考虑最有用的个人资料是：

直线水平地板，可忽略不计的厚度，上游端或下游端的纸桩。

ii）一个直的水平地板在床下凹陷，但没有任何垂直切断。

1. 一个直的水平楼层，厚度可忽略不计，有些厚度

中间点

以曲线的形式给出了上述轮廓的流动网的数学解。根据曲线，确定各种关键点E，C，E1，C1等的百分比压力。要注意的重要要点是：

1. 桩与地板的连接点{e，c（底部），e1，c1（顶部）}
2. 桩的底部（d），和
3. 在凹陷底板的情况下，底角（d，d'）的连接

只要实现了以下更正，简单表单的关键点的百分比压力将对任何复杂的配置文件有效：

• 对桩相互干扰的校正
• 校正楼层的厚度
• 校正坡度的坡度

Khosla理论的矫正解释了

对桩相互干扰的校正

让B1 =两个桩1和2之间的距离，

D =桩线（2）的深度，必须确定在深度d的相邻桩（1）上的影响

B =不透水楼层的总长度

C =由于干扰引起的校正。

校正作为头部的百分比施加

当该点被认为是在干扰桩的后部并且用干扰桩中沿前向或流动方向考虑的点处的负数时，该校正是正的。

校正楼层厚度

假设楼层具有可忽略厚度的标准配置文件。因此，从曲线计算的百分比压力的值对应于地板的顶层（E1 *，C1 *）。但是，地板和桩的结点位于地板的底部（E1，C1）

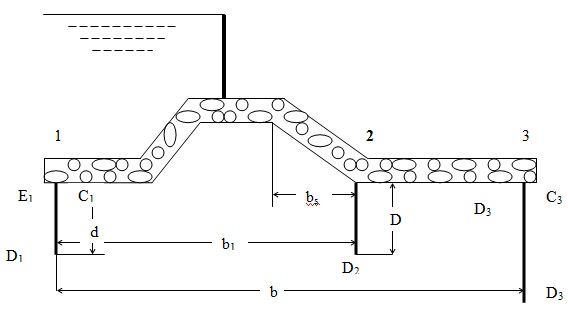
通过假设来自点E1 *至D1的压力的直线变化和D1至C1，通过将实际点E1和C1处的压力内插。

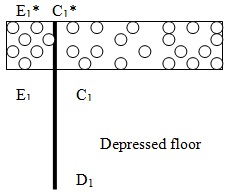
E1的校正压力应小于计算的压力T E1 *。因此，E1的压力的校正将是阴性的。因此，也适用于C1的压力。

铺面坡度

对倾斜的不透水地板的校正对于流动方向上的下斜率和负面的流动方向上的负面的校正。

不。	斜坡= ver：rhorp	校正为压力的百分比
1	1：1	11.2
2	1：2	6.5
3.	1：3	4.5
4.	1：4	3.3
5.	1：5	2.8
6.	1：6	2.5
7.	1：7	2.3
8.	1：8	2.0

校正因子必须乘以斜率的水平长度，并且除以倾斜地板之间的两个极之间的距离。在上图中，可以仅应用于斜率的校正仅针对点E2。随着点E2在流动方向上终止于下降斜率，校正将是正的。更正的价值将是：
C.F.X BS / B1

其中c.f.=校正因子

BS =倾斜地板的水平长度

B1 =桩线之间的水平距离

退出和关键梯度

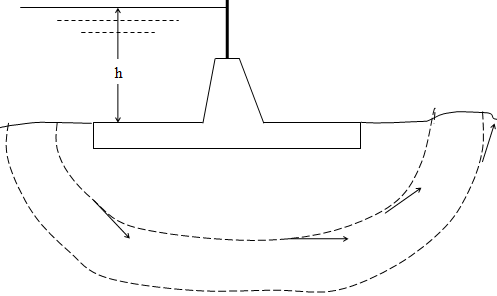
在任何位置渗透亚土的各种水颗粒将施加力量F，这将在任何时候都与流线相切。随着流线向上弯曲，切向力F将具有垂直组件F1。同样在那一点上，由于土壤颗粒的浸没重量，将有向下的力W.因此，在那一点上，颗粒上会有两个力;一个向上的垂直组分F，而另一，淹没重量。显然，如果土壤颗粒不脱落，则浸没重量必须大于向上垂直分量F。任何点的向上垂直分量力与水压梯度DP / DX成比例。

因此，对于土壤的稳定性和预防侵蚀和管道，渗水在下游侧出现时，在出口位置，力F1应小于浸没重量W.换句话说出出口梯度下游结束必须是安全的。

如果在下游侧的出口点，则出口梯度使得力F1就等于土壤粒子的浸没重量，然后调用该梯度临界梯度。安全出口梯度= 0.2至0.25的临界出口梯度。

安全出口梯度的值可以被视为：

• 细砂0.14至0.17
• 粗砂0.17至0.20
• 瓦片0.20至0.25

对于由长度B的地板组成的标准形式，并且其下游端的垂直截止截止值是：

退出梯度ge =（h / d）x