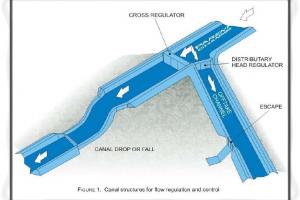
如何设计拦河坝

拦河坝的设计有两个方面:

1. 面流/溢流考虑

2. 地基流动安全性即(根据Bligh的蠕变理论、Lane的加权蠕变理论和Khosla的理论)

1.表面流量/溢出考虑：

如遇溢流因素，须评估/设计以下项目:

1. 设计洪水估算。
2. 拦河坝长度，即(桥台之间的宽度)

3. 倒退
4. Barrage Inflic i.e.上游楼层，D / S楼层，峰值

1.设计洪水估算:

根据结构的使用寿命，对拦河坝的设计洪水(最大洪水)进行了估计。设计洪水估计有50年、100年等。

2.拦河坝长度(桥台宽度b/w):

Lacey的配方可用于固定禁止的长度i.e.p_wQ = 4.75

其中，
Pw =湿周
Q =最大洪水流量

由t可以计算出弹幕长度为:弹幕长度= L.L.C x Pw

式中，
L.L.C = Lacey’s loose coefficient，若未提及，取L.L.C = 1.8

3.退化:

这是河川在经过冲积土后修建挡土墙后出现的一种暂时现象。由于回水效应和深度的增加，水的流速减小，导致沉积负荷的沉积。流过大坝的水含有较少的淤泥，所以水会从下游河床带走淤泥。这导致d/s河床降低到几英里。这就是所谓的倒退。

它可能发生在前几年，床上水平经常恢复他们之前的水平。在几年之内，流过堰的水具有正常的淤泥负荷，并且这个循环逆转。然后由于深度较大，沉积淤泥，D / S床恢复到平衡。渗出值为洪水排放和低放电最大值的最小值。值改变（2 - 8.5）ft。

4.吸积:

这是逆行，通常发生在上游，但也可能发生在逆行周期完成后的d/s。
没有精确的方法来计算回归和吸积的值，但从不同的坝计算的值可以作为一个指导方针。

5.接二连三简介:

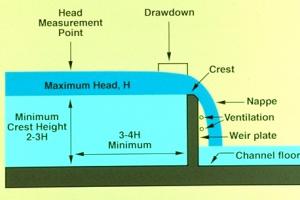
•嵴级别：嵴级别由在嵴上通过设计洪水所需的总部来固定。池塘水平被视为H.F.L.
Maximum scour depth can be calculated from Lacey’s scour formula,

R = 1.35 (q2f) 1/3(抗议)R = 0.9 (q2f) 1/3 (F.P.S)

每单位宽度放电，Q =方法的Qlvelocity，V = QRVelocity头= V22G和放电可以使用放电公式找到，Q = Clh 3/2

式中
C =流量系数取2.03 (M.K.S)， Q =泄洪量，
L =坝顶长度
，H=总能水头= v22g + H
•

设计洪水估算

估计基础

任何给定返回期的设计泛洪通常由频率分析方法估算。将从以下内容中选择适当类型的频率分布：

1. 皮尔逊和对数皮尔逊III型分布
2. Gumbel的极值分布
3. 正常和日志正态分布

应该指出的是，美国联邦机构采用的是Log Pearson III型分布，而普遍认为Gumbel分布适用于巴基斯坦的大多数河流，包括印度河及其支流。

设计重现期

在重要而昂贵的拦河坝结构的设计中，往往采用100年的回返期，而这些拦河坝结构的破坏可能造成非常严重的后果。因此，在业主同意的情况下，设计洪水将按100年、200年和500年的不同重现期进行估算。然而，如实际记录的洪峰流量超过有关返回期计算的流量，则须进行设计检讨。

液压单元

尺寸和单位的属性用于解决液压问题表达三个基本量的质量(M),长度(L)和时间(T)。所有的分析和设计将受到打击还得追溯到Foot-Pound-Second单位制和转换的单位将根据需要的重要成果。

拖动宽度

三个因素决定了拦河坝的宽度。它们是设计洪水、莱西设计宽度和松动系数。一般认为，通过限制水道，可以消除上游的浅滩形成。然而，它增加了放电强度，因此结构的截面变得更重，过高的闸门高度和成本增加，虽然结构的长度减少。

设计洪水在2.2节中讨论，其他两个注意事项将在下面的章节中讨论。

莱西的设计宽度

Lacey的单通道设计或稳定宽度表示为:

W = 2.67 v Q

Q是设计流量，单位是cusecs (ft^3./秒)。

拦河坝的设计宽度超过W，部分是为了容纳漫滩泄洪，部分是为了利用拦河坝本身造成的阻塞所导致的河道水流分散。

松动的因素

实际宽度与制度宽度的比率是“松散因子”，第三参数影响拦阻宽度。所用的值从1.9到0.9变化，在较早的设计中应用的较大因素。通常，它从1.1到1.5变化。从这些结构的性能来看，某些季度出现的感觉，具有高松动因素，结构上游的浅层形成趋势，这导致损坏和维护问题。顾问将使用最合适的松动因素，以提供合理的灵活性，将不良影响保持在最低限度。

涌进

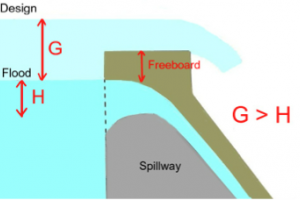
拦河坝上游的最高洪水位因拦河坝的建设而上升，称为溢流。流入虽然在开始时仅限于拦河坝上方的一小段河流，但逐渐向上游延伸，直到拦河坝上游河流的最终斜坡建立。

在建立在冲积砂上的拦河坝/堰的设计中，溢流限制在3至4英尺之间——更常见的是3英尺。流入量的大小决定了导堤的最高水位和长度，以及防洪堤的最高水位和断面。它将支配动态作用，因为从上游到下游水平的流入或下降越大，作用就越大。它还可以控制驻波的深度和位置。通过提供一个高流量，弹幕的宽度可以缩小，但训练工作的成本将上升，失败的风险将增加侧翼。选择和采用一个现实的媒介价值是势在必行的。

尾水额定曲线

通过对水位流量数据的分析，建立坝体尾水额定值曲线。新设计的建议尾水位将由现有的平均尾水位减去设计的回归值来确定。

佳洁士的水平

在漏洞的溢出部分的溢流部分的放电方面，嵴水平的固定明显相关的允许松散因子和排出强度。在考虑所有相关因素和类似结构上的经验之后，将修复嵴水平，以便在正常的池塘水平上通过所有盖茨完全打开的普通池塘水平。

通过拦阻（自由流动条件）放电

通过在游离流动条件下通过阻塞的放电应从下式获得：

Q = c.l。H3./ 2.…(1)

在那里,

Q =以cusecs为单位的排放

C =放电系数

L =大坝畅通水道(英尺)

H =导致流量以英尺为单位的总扬程

C值一般取为3.09，但对于模块化堰运行(Gibson)， C值可能接近最大值3.8。然而，设计一个新的拦河坝将由物理模型研究确定。

通过拦河坝的排放(淹没水流情况)

堰上的流量是模块化的，当它与下游水位的变化无关。为此，下游能量头在波峰上（e₂)不能超过上游能量头的80% (E₁）。比例（e₂/ E.₁)为“模比”，“模极限”为值(E₂/ E.₁= 0.80)的模量比，当流量停止自由流动时。

FANE的曲线

对于浸没（非模块化）流程，上述等式（1）中的放电系数应乘以减少因子。减少因子取决于模块化比（e₂/ E.₁)和减除系数的值(C_r）在下表中给出的是FANE曲线（REF：2.3），适用于有上游斜坡和斜坡下游的堰2H：1V或奉承：

浸没式放电由等式给出：

q = 3.09。Cr。b生产11.5

吉布森曲线

Q = C 'bE1.5

地点:

超过波峰淹没流量(cusecs)

C' =水下流量系数

B =堰宽(英尺)

E₁=上游能量头高于顶部

= h1+ V.12/ 2 g(英尺)

对于浸没放电，自由流量放电系数（C = 3.80）乘以减少因子（C'/ C）。系数因子取决于模块化比（H / e），其中他的下游流量在波峰上方。下表中给出的减少因子“C'/ C”的值来自适用于广泛的Crested堰的Gibson曲线：